期末
字数
1158 字
阅读时间
5 分钟
一、求逆元
- 视频链接:扩展欧几里得求逆元(辗转相除法) 使用扩展欧几里得方法来求逆元(前提:
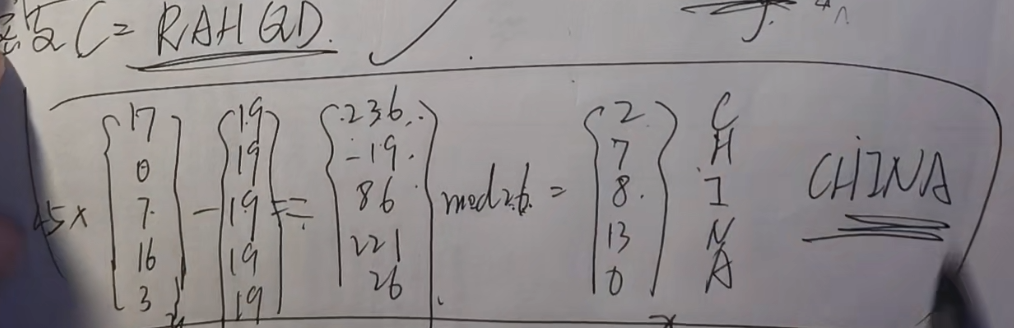
),其中使用到了辗转相除法,如: 每次运算的式子均为:余数 = 被除数 - 商×除数,再将此次的商作为下一个式子的被除数,余数作为下一个式子的除数 - 举个例子,当
时,使用辗转相除法如下: - 例式如下:首先用
得到 商:2,余数为4,则辗转相除法的式子为: - 继续使用上一个式子的除数和余数去做运算,用大数去除以小数,即:
, 商为1,余数为1,式子为:,直到式子左侧得到的余数为 1 - 如此得到最终式子后,再使用上面的式子进行代换,即: 1 = 5 - 4×1 = 5 - (14 - 5×2) = 5×3 - 14,故 5 的逆元为 3
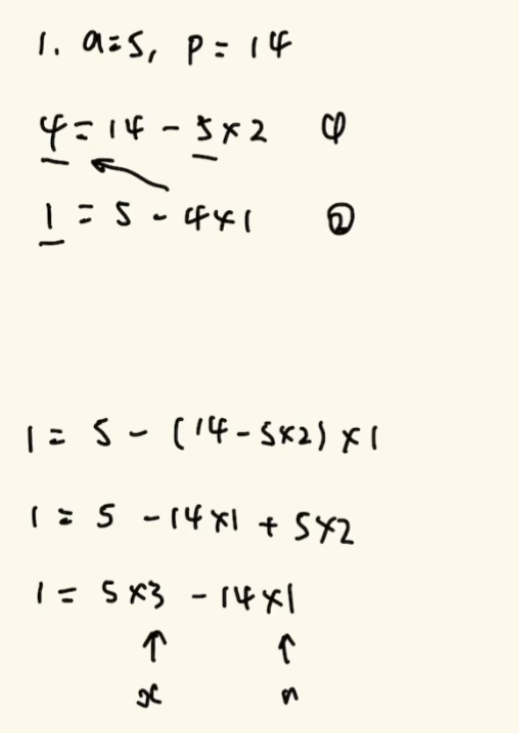
- 例式如下:首先用
二、数字签名,公钥加密和私钥加密,消息认证
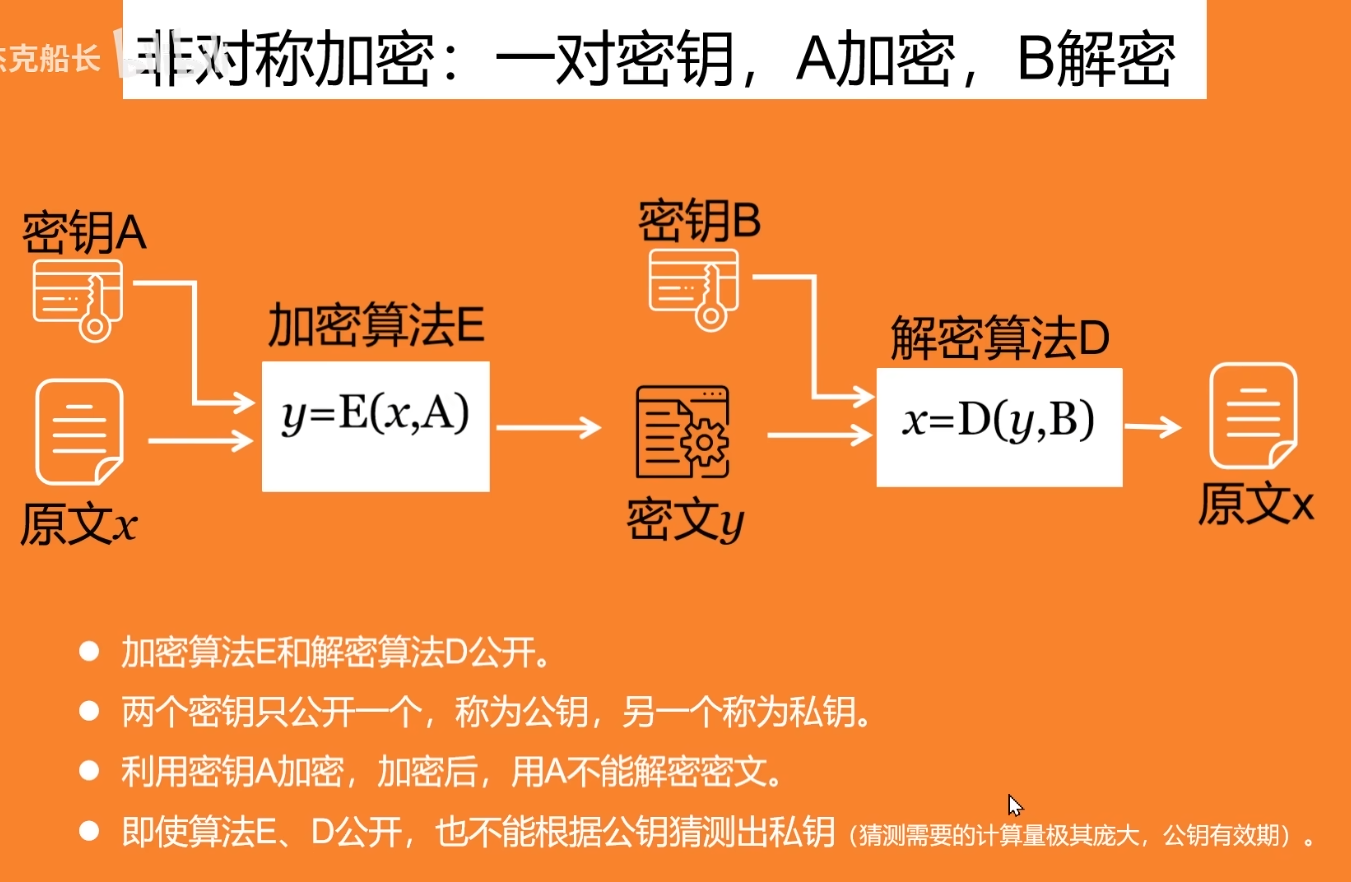
- 数字签名技术原理解析:
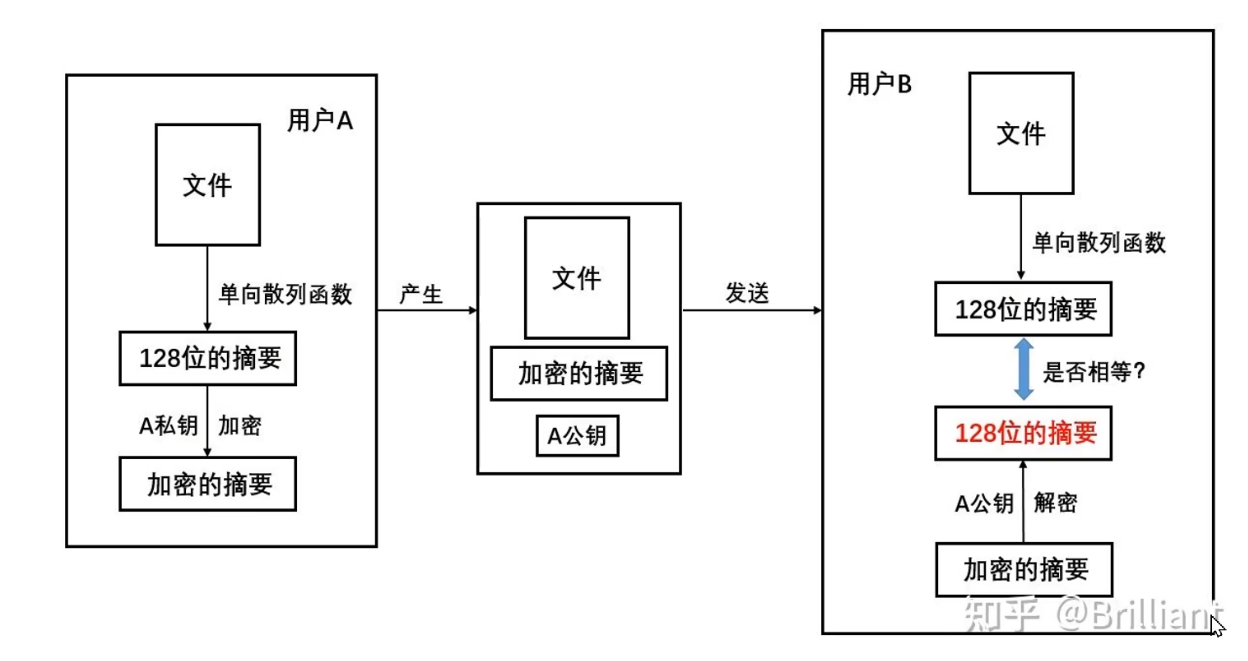
- 其中,公钥是是用户向权威机关CA申请的,无法抵赖
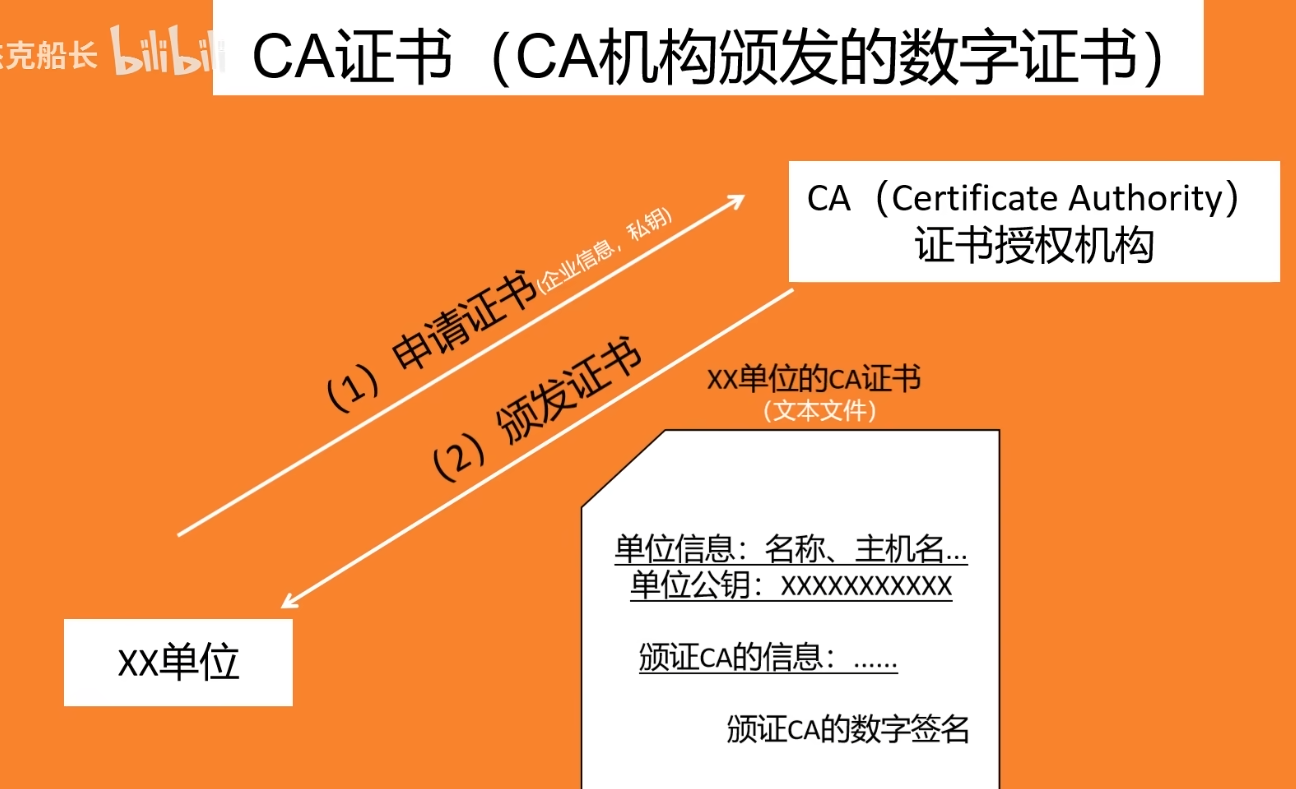
- 该单位的私钥是由该单位自己产生的一串随机数并存储在单位计算机内,将私钥和企业信息发送给CA后,CA机构会根据私钥生成对应的公钥,实际上,发送给CA机构的并不是该单位的实际公钥,而是与公钥一共生成的证书签名请求文件(CSR文件),而CA机构拿到的所谓私钥也就是这个CSR文件
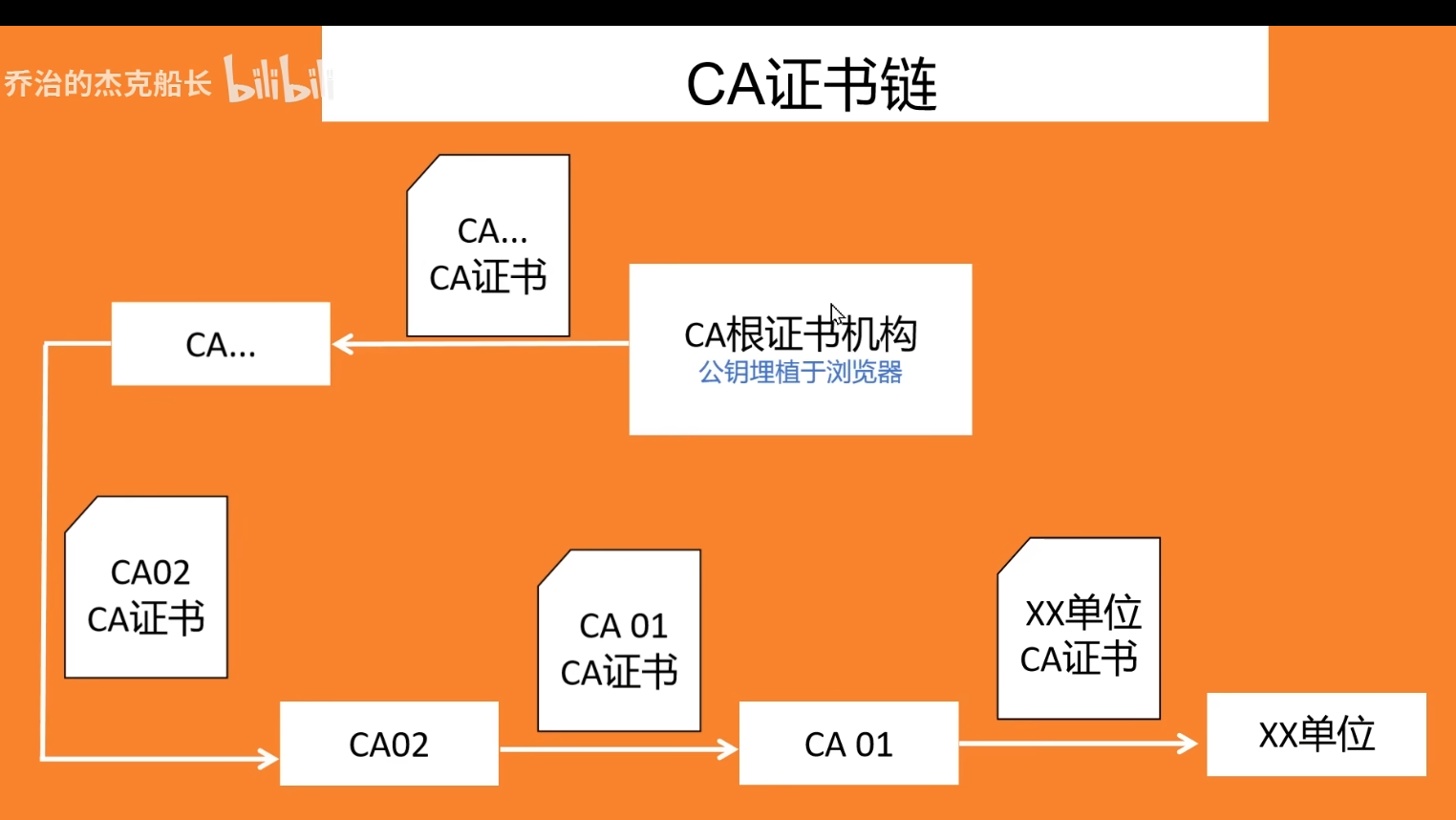
- 如何保证CA的权威性:每次都由更高一级的CA来给低一级的CA机构发证书来担保,最高可追溯到CA根证书机构


- 其中,公钥是是用户向权威机关CA申请的,无法抵赖
(一)Elgamal加密算法
- 密钥生成:
- 选择一个大质数 p,选择 p 的本原元 g
- 选择一个随机数
(p阶循环阶群) - 本原元:
- g 是群中的生成元
,
- 本原元:
- 公钥:
- 私钥:
- 加密过程:
- 选择一个随机数
,m 为消息 - 计算
, - 密文为:
- 选择一个随机数
- 解密过程:
- 签名过程:
- 验证签名:
三、RSA加密
- 非对称加密算法
- 计算方法:给定 n, e 的值和用户密文,求明文?
- 选择两个大素数 p 和 q,计算
和 - 取素数 e,
并且 - 求 d,使得
,最好使用使用扩展欧几里得算法的辗转相除法,或可用公式: (k 是一个整数) - 生成公钥 (e, n) 和私钥 d,d 叫做 e 的模反元素
- 公钥加密:
- 私钥解密:
- 选择两个大素数 p 和 q,计算
四、ECC加密
- 参数选择:
- 选取一条椭圆曲线,得到
,即:代表椭圆: 的参数,将明文消息嵌入曲线得到点 。 的生成元是 , 和 是公开参数
- 选取一条椭圆曲线,得到
- 产生公钥和私钥:用户选取整数
为私钥, 为公钥 - 加密:选随机正整数
,密文为 ,其中, - 解密:
- 具体解释过程:
- 具体解释过程:
- 其中,加密和解密过程计算需要对生成元个数取模,即:
,其中 代表生成元的个数 - 椭圆曲线上两点相加公式:
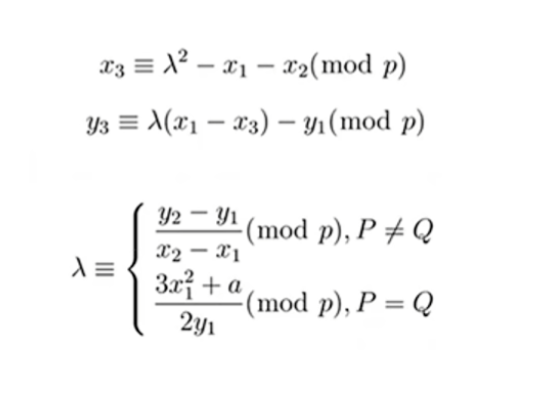
五、仿射加密
- 仿射加密是单表加密的一种
- 密钥:
,求出: - 加密公式:
- 解密公式:
- 其中, a 与 m 互质,
是 a 在 群中的a乘法逆元
- 其中, a 与 m 互质,
例题
- 题干:

- 加密:
 字母下标从0开始
字母下标从0开始 - 解密: