二维差分

字数

391 字

阅读时间

2 分钟

• 假设存在 $n\times n$ 的矩阵，则：
  • 原数组为：$a[N][N]$
  • 其差分数组为：$f[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$
  • 得到原数组的方式：
    • $f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1]$

公式计算（在树状数组中的应用）

假设存在二维差分数组，那么要求其前缀和，就要通过二维计算，但在数据量大时，无法通过两次前缀和得到结果，会超时，所以需要维护两个树状数组。计算过程如下： $b_k=\sum _{i=1}^k\sum _{j=1}^i{b}_j=\sum _{i=1}^k{b}_j\ast (k-j+1)=(k+1)\sum _{i=1}^k{b}_j-\sum _{i=1}^k{b}_j\ast j$ 因为$\sum _{j=1}^i{b}_j$ 的第一项 $b_1$ 会被取 k 次，第二项 $b_2$ 会被取 k - 1 次，所以总结规律即可得出结论：$\sum _{i=1}^k{b}_j\ast (k-j+1)$

• 相关例题解析地址：P1438 无聊的数列 - 洛谷 (luogu.com.cn)

应用

• 一图示：
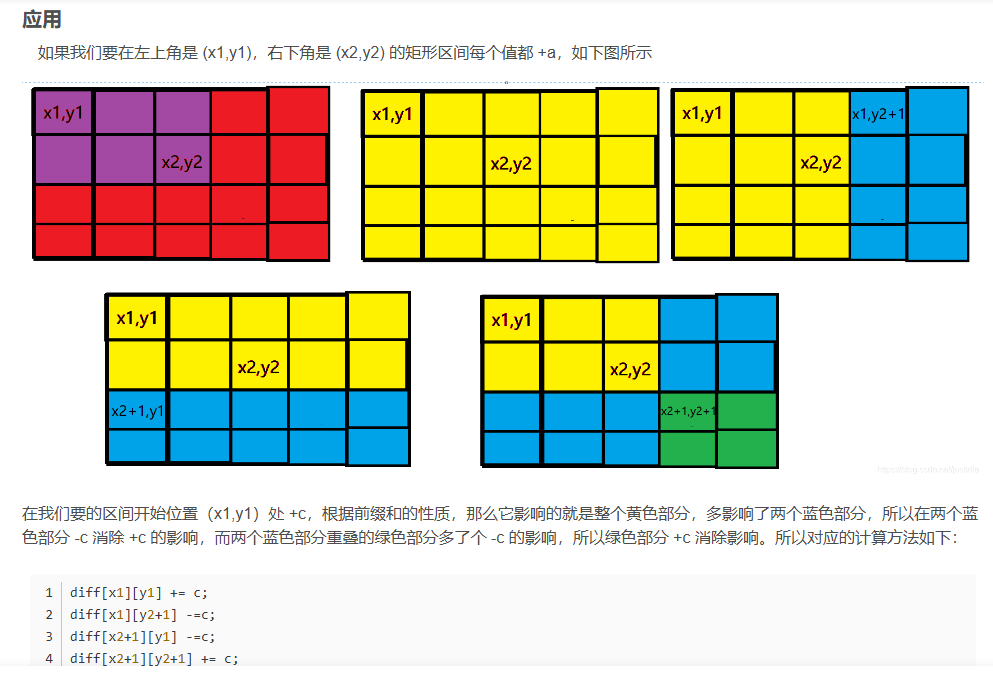
• 说明：
  • 在我们要的区间开始位置（x1,y1）处 +c，根据前缀和的性质，那么它影响的就是整个黄色部分，多影响了两个蓝色部分，所以在两个蓝色部分 -c 消除 +c 的影响，而两个蓝色部分重叠的绿色部分多了个 -c 的影响，所以绿色部分 +c 消除影响。所以对应的计算方法如下：

diff[x1][y1] += c;
diff[x1][y2+1] -=c;
diff[x2+1][y1] -=c;
diff[x2+1][y2+1] += c;

贡献者

freeway348

文件历史

最后编辑于 大约 1 个月前查看完整历史

01996-OS