知识点汇总

字数

2008 字

阅读时间

9 分钟

---

一、基本逻辑

1. 如果 $A\Rightarrow B$，称A是B的充分条件，B是A的必要条件
2. 如果 $A\iff B$，称A是B的充要条件
3. 如果 $A\nLeftrightarrow B$ ，称A是B的既非充分也非必要条件，也称为无关条件

• $\bar{A}$ 是 $A$ 的对立判断
• 公式
  1. 若 $A\Rightarrow B$，则 $\bar{B}\Rightarrow \bar{A}$；原命题成立，即可推出其逆否命题也成立
  2. $\overline{A\cup B}=\bar{A}\cap \bar{B}$
  3. $\overline{A\cap B}=\bar{A}\cup \bar{B}$
     • 第二、三两点就是德·摩根律，也称为对偶律

二、解析式的定义/概念

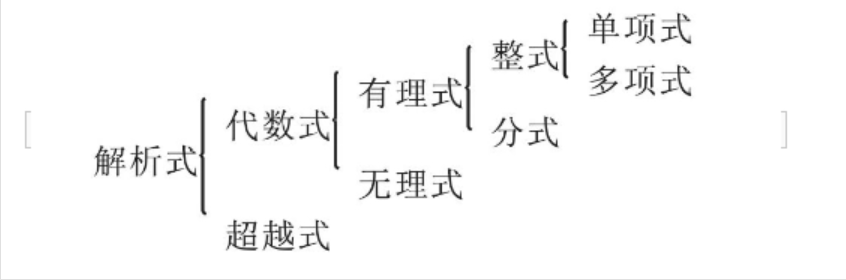
• 单项式：数和字母的积组成的代数式，其中数叫系数，所有字母的指数和叫次数，如：$2a,3b^2,-ab,0$，则 $2a$ 中，2是系数，$2a$ 叫一个单项式；$-ab$ 中，-1是系数，$-ab$ 叫二次单项式；0中，0是系数，0叫零次单项式
• ⭐多项式：单项式的和叫多项式，所有单项式中的最高次数，叫多项式的次数，如：$2a+3b^2-ab$，其中，$2a,3b^2,-ab$ 叫多项式的项，$2a+3b^2-ab$ 是二次多项式（因为单项式的最高次数是2）
• 整式：单项式与多项式统称整式
• ⭐分式（注意区分系数为分数的单项式）：设$A,B$为整式，$B$中有字母，则$\frac{A}{B}$叫分式。若求分式的定义域，记得考虑$B\ne 0$ ；当$A$ 的次数小于 $B$ 的次数时，称为真分式，否则称为假分式
• 有理式：分式和整式统称有理式
• 无理式：含有字母的根式运算的代数式（字母在根号内），如：$\sqrt{2x}$ 是无理式，$\sqrt{2}x$是有理式
• 代数式：有理数和无理数的统称，即：由数与字母作有限次加、减、乘、除、开方、乘方等初等代数运算得到的式子
• 超越式：含有字母的指数为无理数的指数运算、对数运算、三角运算和反三角运算的解析式，以上运算也称为初等超越运算，以区分初等代数运算，如：$\ln (x^2+y^2),\arctan x,a^{\sqrt{2}}$ 等均为超越式
• 解析式：代数式和超越式的统称

运算

• 整式运算：使用系数竖式计算法，详情见基础30讲P6
• 分式运算：先进行因式分解，消去公因式（如果可以的话），再用多项式长除法，详情见基础30讲P9 （同页底下注意看$(f(x),g(x))$的解释）

三、无理式运算

• $\sqrt[n]{a}$ 称为a的n次算数根，但要注意：求解与求算数根不同
• 性质：设 $a\ge 0,b\ge 0,m,n,k\text{为正整数}$
  1. $\sqrt[n]{a^m}=\sqrt[kn]{a^{km}}$
  2. $\sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}$
  3. $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}(b\ne 0)$
  4. $(\sqrt[n]{a}{)}^k=\sqrt[n]{a^k}$
  5. $\sqrt[k]{\sqrt[n]{a}}=\sqrt[kn]{a}$
• 重要结论：
  1. 🌟$\sqrt{a^2}=|a|$ （详情见基础30讲P10）
  2. 有理化
     • 无理式·无理式（与上一个无理式为共轭式）= 有理式，如：$(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b$
       • 注意：无理式相乘不一定会得到有理式
     • 🌟重要公式：$(\sqrt[3]{a}\pm \sqrt[3]{b})(\sqrt[3]{a^2}\mp \sqrt[3]{ab}+\sqrt[3]{b^2})=a\pm b$

四、一元 $n$ 次方程的根与系数关系

• 设$f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0=0(a_n\ne 0)$的根为$x_1,x_2,x_3,\cdots ,x_n$，则
  • $x_1+x_2+\cdots +x_n=-\frac{a_{n-1}}{a_n}$ // 任意1个根的组合之和
  • $x_1{x}_2+x_1{x}_3+\cdots +x_2{x}_3+x_2{x}_4+\cdots +x_{n-1}{x}_n=\frac{a_{n-2}}{a_n}$ // 任意2个根的组合之和
  • $\cdots \cdots$
  • $x_1{x}_2{x}_3{x}_4{x}_5\cdots x_n=(-1{)}^n\cdot \frac{a_0}{a_n}$ // 任意n个根的组合之和
• 当n=2时，有韦达定理：即：$f(x)=a{x}^2+bx+c(a\ne 0)$的两个根$x_1,x_2$的关系为：
  1. $x_1+x_2=-\frac{b}{a}$
  2. $x_1{x}_2=\frac{c}{a}$

五、不等式

1. 伯努利不等式（基本不等式，Ber-不等式）：$(1+x{)}^n\ge 1+nx,x>-1$
2. 均值不等式：$\frac{2}{\frac{1}{a}+\frac{1}{b}}\le \sqrt{ab}\le \frac{a+b}{2}\le \sqrt{\frac{a^2+b^2}{2}}(a,b>0)$ （从左到右以此是：调和平均值，几何平均值，算数平均值，均方根）
   • 不等式等号成立条件：当 $a=b$ 时等号成立
   • 若存在三元，即：$\sqrt[3]{abc}\le \frac{a+b+c}{3}\le \sqrt{\frac{a^2+b^2+c^2}{3}}$
3. 三角不等式：$||a|-|b||\le |a\pm b|\le |a|+|b|$
   • 若：$|a+b|\le |a|+|b|$ ，则当$a\cdot b\ge 0$ 时等式成立，当$a\cdot b<0$ 时不等式成立
   • 若绝对值内为减法式子，则成立条件反过来
4. 🌟柯西不等式：$({a_1}^2+{a_2}^2+\cdots +{a_n}^2)({b_1}^2+{b_2}^2+\cdots +{b_n}^2)\ge (a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n{)}^2$
   • 🌟要注重柯西不等式的证明，明白柯西不等式到底是怎么得出的，证明过程见基础30讲P14
   • 一般常考当n=2时的不等式，即：$({a_1}^2+{a_2}^2)({b_1}^2+{b_2}^2)\ge (a_1{b}_1+a_2{b}_2{)}^2$
   • 当且仅当：$\frac{a_1}{b_1}=\frac{a_2}{b_2}=\cdots \frac{a_n}{b_n}$时，等号成立
   • 不等式应用见基础30讲P19，例26
5. 🌟🌟🌟二次函数的不等问题：详情见基础30讲P14^[1]
6. 函数对称问题见基础30讲P22处的图表^[2]
7. 函数图像变换问题：
   • $y=f(x)$
     • $\Rightarrow y=f(x)+y_0$ 向上移动$y_0$ (若$y_0<0$则向下移动)
     • $\Rightarrow y=f(x+x_0)$ 向左移动$x_0$
     • $\Rightarrow y=kf(x)$ 垂直伸长至 $k$ 倍（k>0）
     • $\Rightarrow y=f(kx)$ 水平伸长至 $\frac{1}{k}$ 倍 (k>0)
     • 
8. 三角函数变换：若遇到 $a\sin x+b\cos x$，则可先提取 $\sqrt{a^2+b^2}$ ，可将原式子化简为：$\sqrt{a^2+b^2}(\frac{a}{\sqrt{a^2+b^2}}\sin x+\frac{b}{\sqrt{a^2+b^2}}\cos x)=\sqrt{a^2+b^2}\sin (x+\varphi )$ ，该思路是由三角函数图像性质得来，图像解释如下：
   

六、数列

处理数列的几种办法

• 数列$\{x_n\}$ 可看作是自变量为正整数 $n$ 的函数：$x_n=f(n),n\in N_{+}$ ，当自变量 $n$ 依次取$1,2,3，\cdots$ 一切正整数时，对应的函数值就排列成数列$\{x_n\}$
  • 数列的项数是无穷多的，即为：无穷数列
• 🌟数列分类：
  1. 等差数列：
     1. 首项为$a_1$，公差为 $d(d\ne 0)$ 的数列称为等差数列
     2. 通项公式：$a_n=a_1+(n-1)d$
     3. 前n项的和$S_n=\frac{n}{2}[2a_1+(n-1)d]=\frac{n}{2}(a_1+a_n)$
        • ⭐若未给出$a_1\text{和}d$ ，则可尝试列举$a_1+a_2\text{与}{a}_2+a_3$ 两式子解出
  2. 等比数列：
     1. 首项为$a_1$，公比为 $q(q\ne 0)$ 的数列称为等比数列
     2. 通项公式：$a_n=a_1{q}^{n-1}$
     3. 前n项的和
        • $S_n=n{a}_1,q=1$
        • $S_n=\frac{a_1(1-q^n)}{1-q},q\ne 1$
        • 常用：$1+q+q^2+\cdots +q^{n-1}=\frac{1-q^n}{1-q}$

七、坐标轴旋转

• 旋转图：
• 证明过程及结论：
• 🌟结论（矩阵计算）（好记）：
  1. 用新坐标（X，Y）来替代旧坐标（x，y）：$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}X\\ Y\end{array}\right)$
     • 即：$x=X\cos \theta -Y\sin \theta ,y=X\sin \theta +Y\cos \theta$
     • 矩阵计算：（A）= (B)(C)
       • (B)的每一行与(C)的每一列运算，得到(A)的每一行结果(从上到下)
  2. 用旧坐标（x，y）来替代新坐标（X，Y）：$\left(\begin{array}{c}X\\ Y\end{array}\right)=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$
     • 该矩阵变换，相当于将(B)矩阵从第一点（用新坐标替换旧坐标）1.进行了正交变换，即：横变竖，竖变横

八、极坐标

• $\text{极角}\theta \text{与极径}r\text{的范围}：$$r>0,0\le \theta <2\pi$
• 正弦定理：$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R(\text{R为外接圆半径})$
• 余弦定理：
  • $a^2=b^2+c^2-2bc\cos A$
  • $b^2=a^2+c^2-2ac\cos B$
  • $c^2=a^2+b^2-2ab\cos C$

直角坐标与极坐标的关系

• $x=r\cos \theta ,y=r\sin \theta$
• $r=\sqrt{x^2+y^2}$

贡献者

freeway348

文件历史

最后编辑于 2 天前查看完整历史

e5b7e-math_algo

75828-math_q111

7039f-math_OJ

---

1. 重点：二次函数的不等问题 ↩︎

2. 函数对称问题图表 ↩︎