基本概念

字数

539 字

阅读时间

3 分钟

---

字母表

• 字母表 $\mathrm{\Sigma }$ 是一个有穷符号集合
  • 符号：字母、数字、标点符号、...
    • 例如：
      • 二进制字母表：$\{0,1\}$
      • ASCII字符集
      • Unicode字符集

字母表上的运算

1. 字母表 ${\mathrm{\Sigma }}_1$ 和 ${\mathrm{\Sigma }}_2$ 的乘积（product）
   • ${\mathrm{\Sigma }}_1{\mathrm{\Sigma }}_2=\{ab|a\in {\mathrm{\Sigma }}_1，b\in {\mathrm{\Sigma }}_2\}$
     • 例如：$\{0,1\}\{a,b\}=\{0a,0b,1a,1b\}$
2. 字母表 $\mathrm{\Sigma }$ 的 $n$ 次幂：
   • 本质：字母表的$n$次幂 $\Rightarrow$ 长度为$n$的所有符号串构成的集合
3. 字母表 $\mathrm{\Sigma }$ 的正闭包（positive closure）
   • ${\mathrm{\Sigma }}^{+}=\mathrm{\Sigma }\cup {\mathrm{\Sigma }}^2\cup {\mathrm{\Sigma }}^3\cup ...$
     • 例：
     • 本质：字母表的正闭包 $\Rightarrow$ 长度为正数的所有符号串构成的集合
4. 字母表 $\mathrm{\Sigma }$ 的克林闭包（Kleene closure）
   • ${\mathrm{\Sigma }}^{\ast }={\mathrm{\Sigma }}^0\cup {\mathrm{\Sigma }}^{+}={\mathrm{\Sigma }}^0\cup \mathrm{\Sigma }\cup {\mathrm{\Sigma }}^2\cup {\mathrm{\Sigma }}^3\cup ...$
     • ${\mathrm{\Sigma }}^0=\{\epsilon \}$
     • 例：
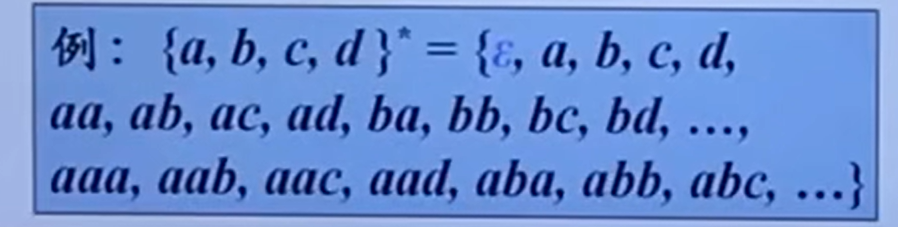
     • 本质：字母表的克林闭包 $\Rightarrow$ 任意字母表（长度可以为零）构成的集合

串

定义

• 设 $\mathrm{\Sigma }$ 是一个字母表，$\mathrm{\forall }x\in {\mathrm{\Sigma }}^{\ast }$，$x$ 称为是 $\mathrm{\Sigma }$ 上的一个串
  • 由此可见，串就是字母表中符号的一个有穷序列
• 串 s 的长度，通常记为 $|s|$ ，是指 s 中符号的个数
  • 例：$|aab|=3$
• 空串是长度为0的串，用 $\epsilon$ （epsilon）表示
  • $|\epsilon |=0$

串上的运算

连接运算

1. 如果 x 和 y 是串，那么 x 和 y 的连接（concatenation）是把 y 附加到 x 后面而形成的串，记作 $xy$
   • 例如：如果 x = dog 且 y = house，那么 $xy=doghouse$
   • 空串是连接运算的单位元（identity）^[1]，即，对于任何串 s 都有：$\epsilon s=s\epsilon =s$
   • 

幂运算

贡献者

freeway348

文件历史

最后编辑于 大约 1 个月前查看完整历史

01996-OS

---

1. 串的连接运算的单位元 ↩︎