以中间某点为峰值的双向上升子序列

字数

1420 字

阅读时间

6 分钟

---

• 原题：Acwing 1014

登山

题目描述

五一到了，ACM队组织大家去登山观光，队员们发现山上一共有$N$个景点，并且决定按照顺序来浏览这些景点，即每次所浏览景点的编号都要大于前一个浏览景点的编号

同时队员们还有另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了

队员们希望在满足上面条件的同时，尽可能多的浏览景点，你能帮他们找出最多可能浏览的景点数么？

输入格式

第一行包含整数$N$，表示景点数量。

第二行包含$N$个整数，表示每个景点的海拔。

输出格式

输出一个整数，表示最多能浏览的景点数。

数据范围

$2\le N\le 1000$

输入样例

8
186 186 150 200 160 130 197 220

输出样例

4

---

题解

思路：

根据题意：需要满足以下几个条件：

1. 按照编号递增的顺序来浏览 $\Rightarrow$ 必须是子序列
2. 连续浏览的相邻两个景点的高度不能相同
3. 一旦开始下山，就不再往上走了 $\Rightarrow$ 走过的路线一定是先上升再下降 路线形如： 目标：要求求出最多能浏览多少个景点？

分析：闫氏DP分析法

具体思路：从a[1]开始一直到a[n]，将所有满足该路线形状的子序列共分为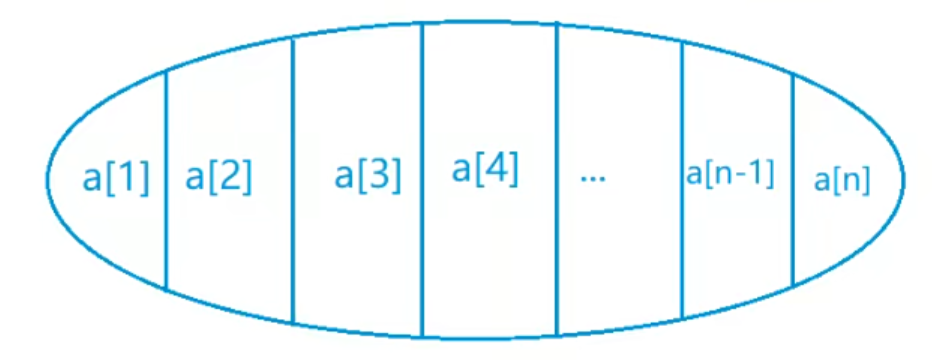$n$类，即：讨论以a[k]为峰值点的路线的所有情况，再将所有情况的答案取最大值即可 并且由于在峰值点左侧和右侧的登山路线是相互独立、互不影响的，所以只要求出左侧路线的最大值和右侧路线的最大值即可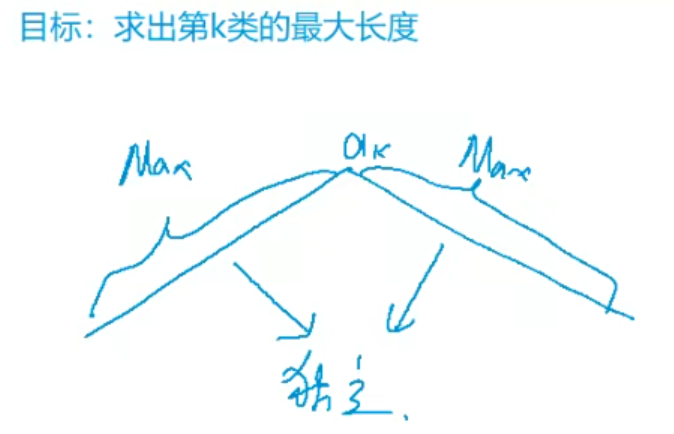

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n;
int f[N], g[N];
int a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];

    // 从前往后求解最长上升子序列问题 ------ 正向LIS
    for (int i = 1; i <= n; i ++)
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++)
            if (a[i] > a[j])
                f[i] = max(f[i], f[j] + 1);
    }

    // 从后往前求解最长上升子序列 ------ 反向LIS
    for (int i = n; i; i --)
    {
        g[i] = 1;
        for (int j = n; j > i; j --)
            if (a[i] > a[j])
                g[i] = max(g[i], g[j] + 1);
    }

    // 求解最大值
    int res = 0;
    for (int i = 1; i <= n; i ++)
        res = max(res, f[i] + g[i] - 1); // 因为以 a[i] 为峰值，且正向LIS和反向LIS的求解过程中均包含了a[i]这个景点，重复了，所以要减 1
    cout << res;
    
    return 0;
}

---

原题：ACwing 482

变形题：合唱队形

题目描述

$N$ 位同学站成一排，音乐老师要请其中的 $(N-K)$ 位同学出列，使得剩下的 $K$ 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 $K$ 位同学从左到右依次编号为 $1，2\dots ，K$，他们的身高分别为 $T_1，T_2，\dots ，T_K$，  则他们的身高满足 $T_1<\dots <T_i>T_{i+1}>\dots >T_K(1\le i\le K)$。

你的任务是，已知所有 $N$ 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入格式

输入的第一行是一个整数 $N$，表示同学的总数。

第二行有 $N$ 个整数，用空格分隔，第 $i$ 个整数 $T_i$ 是第 $i$ 位同学的身高(厘米)。

输出格式

输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列。

数据范围

$2\le N\le 100$,
$130\le T_i\le 230$

输入样例：

8
186 186 150 200 160 130 197 220

输出样例：

4

解析：

本题思路与登山一致，登山求的是从左到右过程中，以某一个景点为最高的峰值时，能经过的最多的景点的数量。 而本题则是在此基础上的一点更改，换成登山的理解就是：找到符合要求的能经过的最多的景点数以后，再求出没去的景点数并输出

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n;
int f[N], g[N];
int a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];

    // 从前往后求解最长上升子序列问题 ------ 正向LIS
    for (int i = 1; i <= n; i ++)
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++)
            if (a[i] > a[j])
                f[i] = max(f[i], f[j] + 1);
    }

    // 从后往前求解最长上升子序列 ------ 反向LIS
    for (int i = n; i; i --)
    {
        g[i] = 1;
        for (int j = n; j > i; j --)
            if (a[i] > a[j])
                g[i] = max(g[i], g[j] + 1);
    }

    // 求解最大值
    int res = 0;
    for (int i = 1; i <= n; i ++)
        res = max(res, f[i] + g[i] - 1); // 因为以 a[i] 为峰值，且正向LIS和反向LIS的求解过程中均包含了a[i]这个景点，重复了，所以要减 1
    cout << n - res;
    
    return 0;
}

贡献者

freeway348

文件历史

最后编辑于 大约 1 个月前查看完整历史

01996-OS