知识点
字数
3082 字
阅读时间
13 分钟
一、 极值点的定义:
- 极值点是
局部的概念 - 极值点是左右邻域均有定义(端点处不讨论极值、间断点)
- 常数函数处处都是极值
- 常考“理想”的极值点,即:左邻域递增,右邻域递减;或左邻域递减,右邻域递增
- 间断点也可以是极值点,详情见基础30讲P188
二、单调性和极值的判别
- 设函数
在 上连续,在 可导,则: - 如果在
内 ,且等号仅在有限个点成立,那么函数 在 上严格单调增加 - 如果在
内 ,且等号仅在有限个点成立,那么函数 在 上严格单调减少 - 当在某一点处,连续点A,B,C(微观上)之间的变化率(导数)可能为0,在水平上的差距极其小,但在该点仍然是左小右大
- 导数大于0,一定严格单增,但严格单增不一定导数大于0,详情解释见基础30讲P188
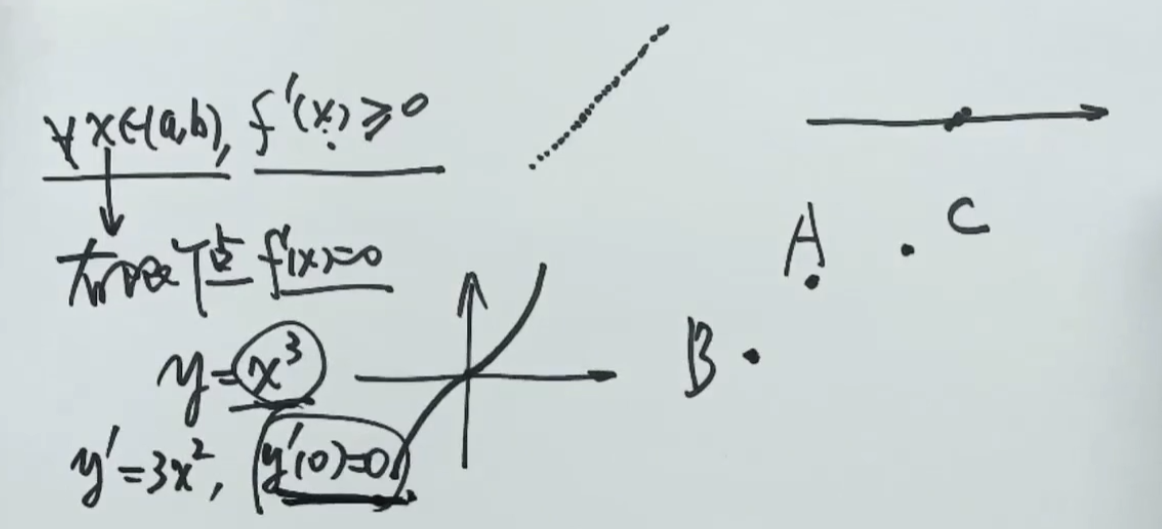
只代表了在 这一点上是可导的,是左小右大,无法证明单调性,且无法证明其他点的单调性 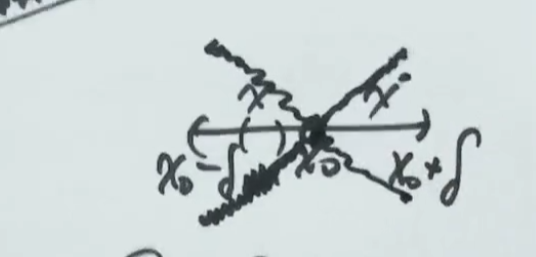
- 如果在
判断不可导点是否为极值点
- 只需要看该点左右的单调性即可
1. 一阶可导时,一阶可导点是极值点的必要条件
证明:第六讲,费马定理- 🌟设
在 处可导,且在点 处取得极值,则必有 - 🌟🌟🌟找极值时的两种情况:1. 驻点;2. 不可导点[1]
- 驻点:
- 不可导点:
不存在
- 驻点:
2. 极值的第一充分条件
- 设
在 处连续,且在 的某去心邻域 内可导
- 若
时, ,而 时, ,则 在 处取得极小值 - 若
时, ,而 时, ,则 在 处取得极大值 - 若
在 和 内不变号,则点 不是极值点 - 换言之,只要变号了,则点
是极值点
- 换言之,只要变号了,则点
注
3. 极值的第二充分条件
- 设
在 处二阶可导,且
- 若
,则 在 处取得极大值 - 若
,则 在 处取得极小值
- 🌟借助保号性推导:
- 设
,由保号性可知: - 当
时, ,从而 ,所以 在 的左邻域单调递减 - 当
时, ,从而 ,所以 在 的左邻域单调递增 所以 在 处取得极小值
- 当
- 同理:当
时, 在 处取得极大值
- 设
4. 极值的第三充分条件
第三充分条件可以说是第二充分条件的推广- 设
在 处 n阶可导,且(注意:m是从 1开始取的)
- 当
n为偶数且时, 在 处取得极大值 - 当
n为偶数且时, 在 处取得极小值
注
1.对平方开根号需要注意:
5. 第二充分条件的注意事项

- 如例5.2,若我们已知
,则可利用第二充分条件判断 为极大值,但需注意,该结论是充分条件,而不是必要条件,故无法反推,所以例5.2不能用该结论反推,因为可能存在 ,使得 ,并且往后导数值均为0,直到某一偶数阶导数 ,这种情况下,仍能得到该例题的条件,所以应该选择选项
三、凹凸性和拐点
1. 凹凸性和拐点的定义[2]


2. 凹凸性与拐点的判别
(1)凹凸性判别
设函数
- 若在
上 ,则 在 上的图形是凹的 - 若在
上 ,则 在 上的图形是凸的
(2)二阶可导时,二阶可导点是拐点的必要条件
🌟设 二阶导为 0 和不可导点 (二阶导不存在)中寻找判断[3]
(3)🌟判断拐点的第一充分条件 ----- 最常用[4]
- 设
在 处连续,且在 的某去心邻域 内二阶导数存在,且在该点的左、右邻域内 变号(无论是否由正变负,还是由负变正),则点 为曲线的拐点
为什么拐点需要在 $x=x_0$ 的**邻域**内二阶可导
因为拐点是凹弧和凸弧的分界点,而凹弧和凸弧的定义又需要用到二阶导数,所以需要在拐点的邻域内二阶可导,判断是否在左、右邻域变号,即可判断是否是凹凸性发生了变化
(4)判断拐点的第二充分条件
- 设
在 的某邻域内三阶可导,且 ,则点 为曲线的拐点 - 同样的,可以用保号性进行推导证明,具体过程可参考极值的第二充分条件,或可见基础30讲P194
(5)判断拐点的第三充分条件
- 设
在 处 n阶可导,且(注意:m是从 2开始取的,注意与极值的第三充分条件区分)[5]- 因为拐点不对一阶导数作要求,所以
m从2开始取
- 因为拐点不对一阶导数作要求,所以
- 当
n为奇数时,点为拐点
四、🌟🌟🌟极值点和拐点的重要结论[6]
以下结论均可直接使用,不必证明- 曲线的
可导点不可同时为极值点和拐点(参考例5.5);曲线的不可导点可以同时为极值点和拐点 - 设多项式函数
,且 ,则当 为偶数时, 是 的极值点;当 为奇数时,点 是曲线 的拐点 - 设多项式函数
,其中 是正整数, 是实数且 两两不等, :一次幂的多项式因式个数 :偶数次幂的因式个数 :奇数次幂的因式个数(n>1) 的极值点个数: ,拐点个数:
- 常规结论:
是 的 重根 ,则 是 的 重根
五、渐近线
1. 铅直渐近线(铅垂渐近线)
- 若
(或 ),则 为一条铅直渐进线
注
此处的
- 无定义点
- 函数定义区间的端点
- 分段函数的分段点
2. 水平渐进线
- 若
,则 为一条水平渐近线;若 ,则 为一条水平渐近线 - 若
,则 为一条水平渐近线(当函数的左、右无穷远极限均相等时)
3. 斜渐近线

求解渐近线的步骤图解[7]: 
六、最值和取值范围
1. 最值的定义
最值是整体概念,有别于极值(极值是局部概念)- 定义:设
为 定义域内一点,若对于 的定义域内任意一点 ,均有 (或 )成立,则称 为 的最大值(或最小值)
极值和最小值的关系
极值点不一定是最值点,最值点也不一定是极值点[8]
- 🌟🌟如果
在区间 上有最值点 ,并且此最值点 不是区间 的端点,而是 内部的点,那么此 必是 的一个极值点[9]
2. 求闭区间上连续函数的最大值和最小值
连续函数
- 求出可疑点的函数值(驻点和不可导点)
- 求出端点的函数值
和 - 比较以上得到的所有函数值,即可得出最大值和最小值
3. 求开区间上连续函数的最大值和最小值
连续函数
- 求出可疑点的函数值(驻点和不可导点)
- 求出区间两端的单侧极限,若
为有限常数,则求 和 (根据区间范围,注意左、右极限) - 比较以上得到的所有函数值,即可得出最大值和最小值
七、作函数图像
一般作图步骤为:
- 确定定义域,考察函数是否有奇偶性,周期性,并用好图像变换(见附录1)
- 用导数工具(一阶导数确定函数的单调区间、极值点;二阶导数确定曲线的凹凸区间、拐点)
- 渐近线
- 作图
注
要学会用直角坐标系的观点画极坐标的图(30讲P205),如:r 作为竖轴,θ 作为横轴,画出变化曲线,根据变化趋势用描点法画出其在极坐标下的图像
八、曲率及曲率半径[10]
- 曲率代表曲线的弯曲程度,曲率越大,弯曲程度越大,能画出的切线圆越小
- 设
二阶可导,则曲线 在点 处的曲率公式为: - 曲率半径:
本章使用到的恒等变形
- 第二步变为 x 是因为
- 第二步变为 x 是因为
