最长上升子序列(LIS)

字数

1013 字

阅读时间

5 分钟

---

原例题讲解

• 原题地址：B3637 最长上升子序列 - 洛谷 | 计算机科学教育新生态
• 同：Acwing 895

题目描述

这是一个简单的动规板子题。

给出一个由 $n(n\le 5000)$ 个不超过 ${10}^6$ 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。

最长上升子序列是指，从原序列中按顺序取出一些数字排在一起，这些数字是逐渐增大的。

输入格式

第一行，一个整数 $n$，表示序列长度。

第二行有 $n$ 个整数，表示这个序列。

输出格式

一个整数表示答案。

输入输出样例

输入 #1

6
1 2 4 1 3 4

输出 #1

4

说明/提示

分别取出 $1、2、3、4$ 即可。

---

解题思路

一、思路

• 方法：闫氏DP分析法
• 具体分析：
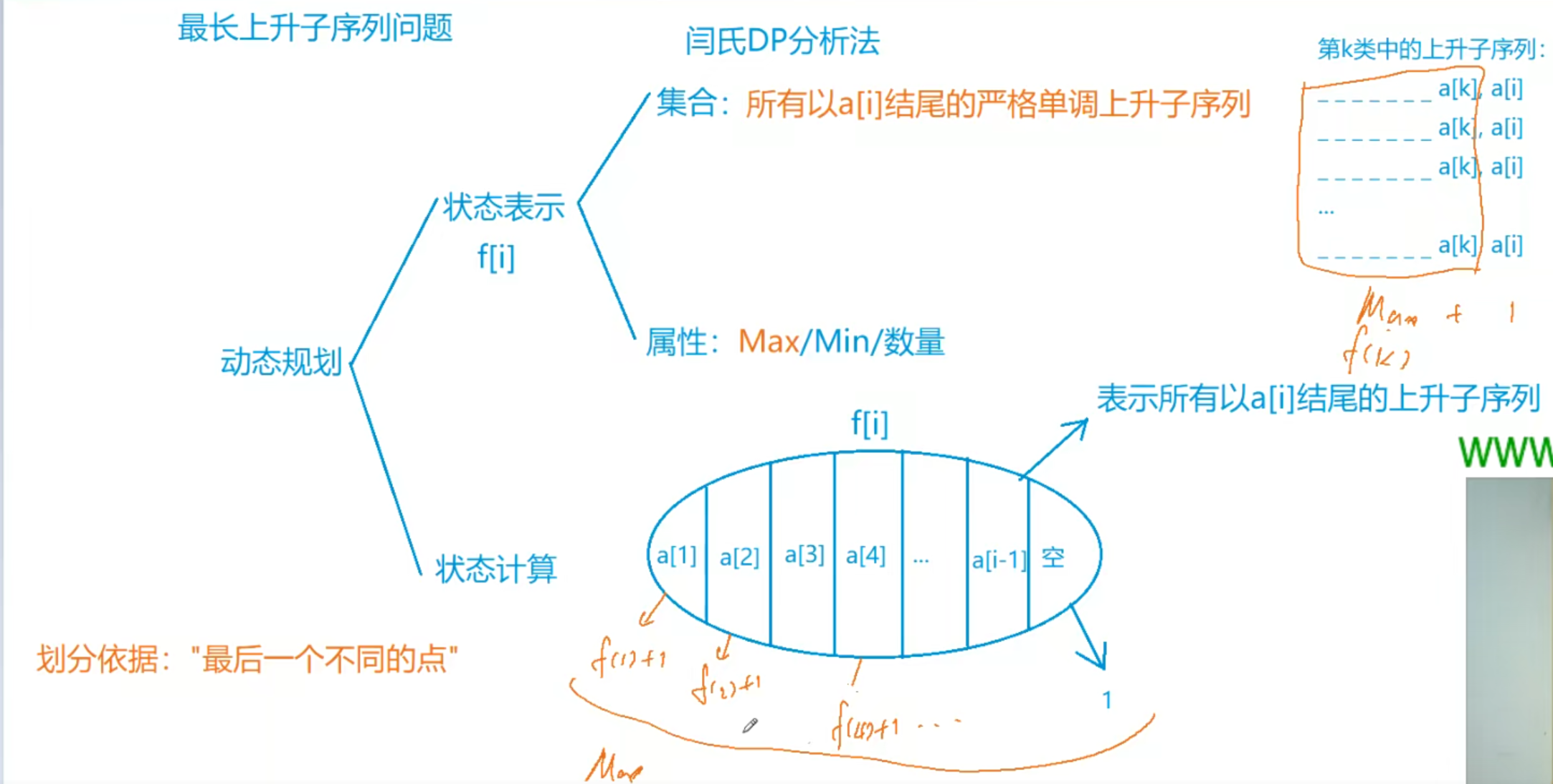
  • 依照倒数第二个不同的值的位置来分类进行讨论（倒数第一为 a[i]，而a[i]都是相同的），根据倒数第二个不同的值的情况来分为 i 类，倒数第二个值可能不存在（即：所有值都相同），也可能是a[1]，a[2]，......，a[i - 1]中的任一个数，只要求出每一个分别的最大值，再进行一次max操作即可

二、代码

1. dp做法

• 时间复杂度$O(n^2)$

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 5010;
int n;
int f[N];
int a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];
    for (int i = 1; i <= n; i ++)
    {
        f[i] = 1; // 先讨论从 f[1] 到 f[i] 的倒数第二个值不存在的情况，即：所有值都相同
        for (int j = 1; j < i; j ++) // 再从头讨论倒数第二个不相同的值为 f[j] 的情况
            if (a[i] > a[j])
                f[i] = max(f[i], f[j] + 1);
    }

    int res = 0;
    for (int i = 1; i <= n; i ++)
        res = max(res, f[i]);
    cout << res << endl;
    return 0;
}

2. 贪心做法

• 时间复杂度$O(nlo{g}_{2}n)$

// 数据量变为 1e5，数据范围在 -2e9 ~ 2e9 之间，所以之前的 O(n^2) 的朴素做法不可行，需要优化
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 2e5 + 10;
int a[N], q[N];

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i ++)    cin >> a[i];
    int len = 0; // 最长上升子序列的长度
    q[0] = -2e9; // 处理边界问题
    for (int i = 0; i < n; i ++)
    {
        int l = 0, r = len;
        while(l < r)
        {
            int mid = l + r + 1 >> 1;
            // 找到已知最长上升子序列中比 a[i] 小的、 最大的值
            if (q[mid] < a[i]) 
                l = mid;
            else r = mid - 1;
        }
        len = max(len, r + 1); // 把 a[i] 加到 q[r] 后边，二分查找后，若存在 q[r + 1]，必定比 a[i] 大，所以可以替换，而如果所有值都比 a[i] 小，那么就会将 a[i] 加到新的一位
        // 因为找上升子序列时：小的数肯定比大的数更好找上升序列，例如：1 3 4 比 1 3 6 更好找到接下来的上升序列
        q[r + 1] = a[i]; // 如果有，就替代，没有就添加
        
    }
    cout << len << endl;
    return 0;
}

代码解析：

维护一个长度为 $len$ 的子序列，其中 $len$ 表示当前子序列的长度。

遍历所有的元素，如果当前元素比子序列中的最后一个元素还大，就将其添加到子序列的末尾，并将子序列长度加1。

否则，我们可以用二分查找找到子序列中第一个大于等于当前元素的位置，将该位置上的元素替换为当前元素，从而保证子序列仍然是上升的。

最终，子序列的长度就是最长上升子序列的长度。

贡献者

freeway348

文件历史

最后编辑于 大约 1 个月前查看完整历史

01996-OS